Improving Flow Matching by Aligning Flow Divergence

Conditional flow matching (CFM) stands out as an efficient, simulation-free approach for training flow-based generative models, achieving remarkable performance for data generation. However, CFM is insufficient to ensure accuracy in learning probability paths. In this paper, we introduce a new partial differential equation characterization for the error between the learned and exact probability paths, along with its solution. We show that the total variation gap between the two probability paths is bounded above by a combination of the CFM loss and an associated divergence loss. This theoretical insight leads to the design of a new objective function that simultaneously matches the flow and its divergence. Our new approach improves the performance of the flow-based generative model by a noticeable margin without sacrificing generation efficiency. We showcase the advantages of this enhanced training approach over CFM on several important benchmark tasks, including generative modeling for dynamical systems, DNA sequences, and videos. Code is available at \href{https://github.com/Utah-Math-Data-Science/Flow_Div_Matching}{Utah-Math-Data-Science}.

RMFlow: Refined Mean Flow by a Noise-Injection Step for Multimodal Generation

Mean flow (MeanFlow) enables efficient, high-fidelity image generation, yet its single-function evaluation (1-NFE) generation often cannot yield compelling results. We address this issue by introducing RMFlow, an efficient multimodal generative model that integrates a coarse 1-NFE MeanFlow transport with a subsequent tailored noise-injection refinement step. RMFlow approximates the average velocity of the flow path using a neural network trained with a new loss function that balances minimizing the Wasserstein distance between probability paths and maximizing sample likelihood. RMFlow achieves near state-of-the-art results on text-to-image, context-to-molecule, and time-series generation using only 1-NFE, at a computational cost comparable to the baseline MeanFlows.

Towards Multiscale Graph-based Protein Learning with Geometric Secondary Structural Motifs

Graph neural networks (GNNs) have emerged as powerful tools for learning protein structures by capturing spatial relationships at the residue level. However, existing GNN-based methods often face challenges in learning multiscale representations and modeling long-range dependencies efficiently. In this work, we propose an efficient multiscale graph-based learning framework tailored to proteins. Our proposed framework contains two crucial components: (1) It constructs a hierarchical graph representation comprising a collection of fine-grained subgraphs, each corresponding to a secondary structure motif (e.g., $α$-helices, $β$-strands, loops), and a single coarse-grained graph that connects these motifs based on their spatial arrangement and relative orientation. (2) It employs two GNNs for feature learning: the first operates within individual secondary motifs to capture local interactions, and the second models higher-level structural relationships across motifs. Our modular framework allows a flexible choice of GNN in each stage. Theoretically, we show that our hierarchical framework preserves the desired maximal expressiveness, ensuring no loss of critical structural information. Empirically, we demonstrate that integrating baseline GNNs into our multiscale framework remarkably improves prediction accuracy and reduces computational cost across various benchmarks.

Learning Decentralized Swarms Using Rotation Equivariant Graph Neural Networks

The orchestration of agents to optimize a collective objective without centralized control is challenging yet crucial for applications such as controlling autonomous fleets, and surveillance and reconnaissance using sensor networks. Decentralized controller design has been inspired by self-organization found in nature, with a prominent source of inspiration being flocking; however, decentralized controllers struggle to maintain flock cohesion. The graph neural network (GNN) architecture has emerged as an indispensable machine learning tool for developing decentralized controllers capable of maintaining flock cohesion, but they fail to exploit the symmetries present in flocking dynamics, hindering their generalizability. We enforce rotation equivariance and translation invariance symmetries in decentralized flocking GNN controllers and achieve comparable flocking control with 70% less training data and 75% fewer trainable weights than existing GNN controllers without these symmetries enforced. We also show that our symmetry-aware controller generalizes better than existing GNN controllers. Code and animations are available at http://github.com/Utah-Math-Data-Science/Equivariant-Decentralized-Controllers.

Learning to Control the Smoothness of Graph Convolutional Network Features

The pioneering work of Oono and Suzuki [ICLR, 2020] and Cai and Wang [arXiv:2006.13318] initializes the analysis of the smoothness of graph convolutional network (GCN) features. Their results reveal an intricate empirical correlation between node classification accuracy and the ratio of smooth to non-smooth feature components. However, the optimal ratio that favors node classification is unknown, and the non-smooth features of deep GCN with ReLU or leaky ReLU activation function diminish. In this paper, we propose a new strategy to let GCN learn node features with a desired smoothness -- adapting to data and tasks -- to enhance node classification. Our approach has three key steps: (1) We establish a geometric relationship between the input and output of ReLU or leaky ReLU. (2) Building on our geometric insights, we augment the message-passing process of graph convolutional layers (GCLs) with a learnable term to modulate the smoothness of node features with computational efficiency. (3) We investigate the achievable ratio between smooth and non-smooth feature components for GCNs with the augmented message-passing scheme. Our extensive numerical results show that the augmented message-passing schemes significantly improve node classification for GCN and some related models.

Deep Learning with Data Privacy via Residual Perturbation

Protecting data privacy in deep learning (DL) is of crucial importance. Several celebrated privacy notions have been established and used for privacy-preserving DL. However, many existing mechanisms achieve privacy at the cost of significant utility degradation and computational overhead. In this paper, we propose a stochastic differential equation-based residual perturbation for privacy-preserving DL, which injects Gaussian noise into each residual mapping of ResNets. Theoretically, we prove that residual perturbation guarantees differential privacy (DP) and reduces the generalization gap of DL. Empirically, we show that residual perturbation is computationally efficient and outperforms the state-of-the-art differentially private stochastic gradient descent (DPSGD) in utility maintenance without sacrificing membership privacy.

Adaptive and Implicit Regularization for Matrix Completion

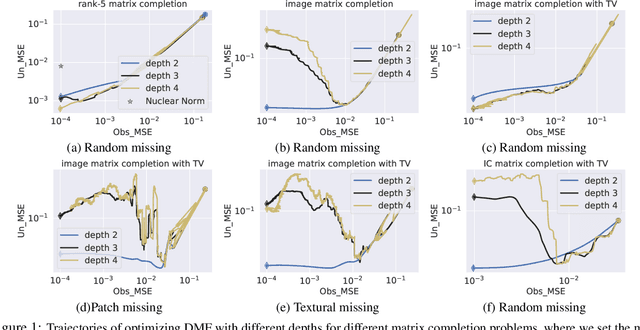
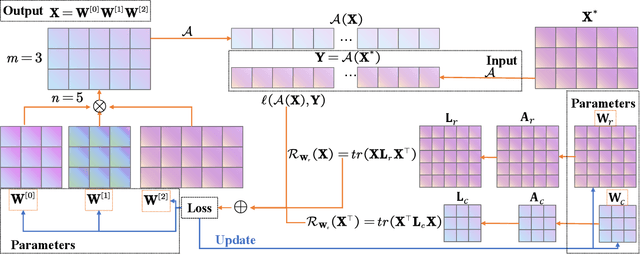
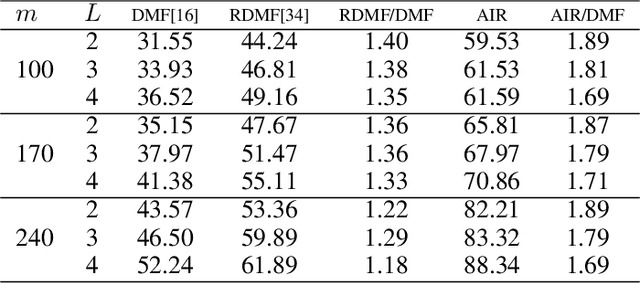
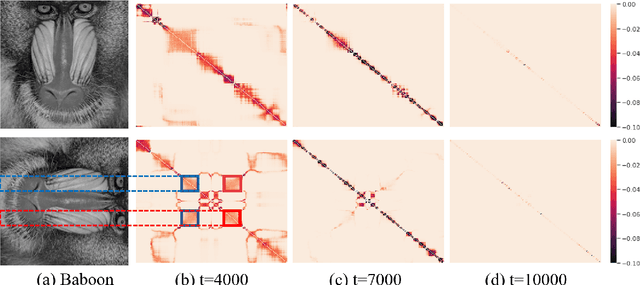
The explicit low-rank regularization, e.g., nuclear norm regularization, has been widely used in imaging sciences. However, it has been found that implicit regularization outperforms explicit ones in various image processing tasks. Another issue is that the fixed explicit regularization limits the applicability to broad images since different images favor different features captured by different explicit regularizations. As such, this paper proposes a new adaptive and implicit low-rank regularization that captures the low-rank prior dynamically from the training data. The core of our new adaptive and implicit low-rank regularization is parameterizing the Laplacian matrix in the Dirichlet energy-based regularization, which we call the regularization AIR. Theoretically, we show that the adaptive regularization of \ReTwo{AIR} enhances the implicit regularization and vanishes at the end of training. We validate AIR's effectiveness on various benchmark tasks, indicating that the AIR is particularly favorable for the scenarios when the missing entries are non-uniform. The code can be found at https://github.com/lizhemin15/AIR-Net.

Momentum Transformer: Closing the Performance Gap Between Self-attention and Its Linearization

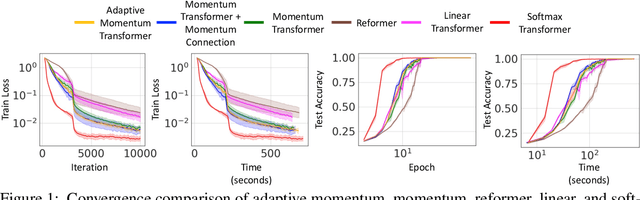
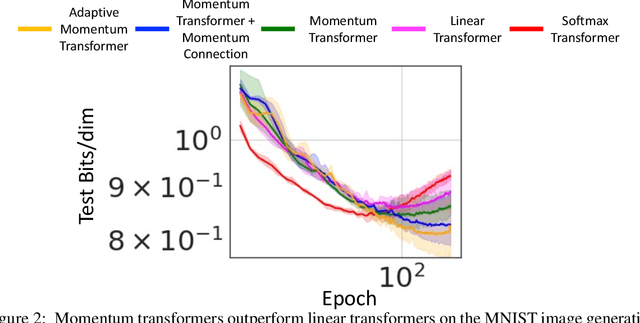
Transformers have achieved remarkable success in sequence modeling and beyond but suffer from quadratic computational and memory complexities with respect to the length of the input sequence. Leveraging techniques include sparse and linear attention and hashing tricks; efficient transformers have been proposed to reduce the quadratic complexity of transformers but significantly degrade the accuracy. In response, we first interpret the linear attention and residual connections in computing the attention map as gradient descent steps. We then introduce momentum into these components and propose the \emph{momentum transformer}, which utilizes momentum to improve the accuracy of linear transformers while maintaining linear memory and computational complexities. Furthermore, we develop an adaptive strategy to compute the momentum value for our model based on the optimal momentum for quadratic optimization. This adaptive momentum eliminates the need to search for the optimal momentum value and further enhances the performance of the momentum transformer. A range of experiments on both autoregressive and non-autoregressive tasks, including image generation and machine translation, demonstrate that the momentum transformer outperforms popular linear transformers in training efficiency and accuracy.

Proximal Implicit ODE Solvers for Accelerating Learning Neural ODEs

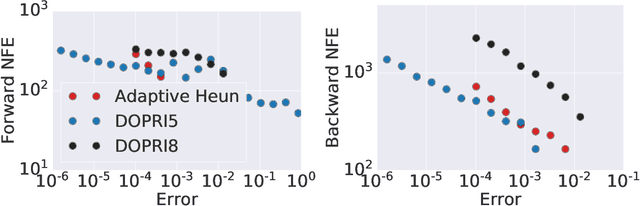
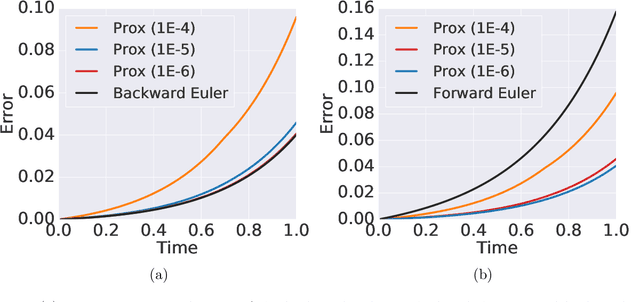
Learning neural ODEs often requires solving very stiff ODE systems, primarily using explicit adaptive step size ODE solvers. These solvers are computationally expensive, requiring the use of tiny step sizes for numerical stability and accuracy guarantees. This paper considers learning neural ODEs using implicit ODE solvers of different orders leveraging proximal operators. The proximal implicit solver consists of inner-outer iterations: the inner iterations approximate each implicit update step using a fast optimization algorithm, and the outer iterations solve the ODE system over time. The proximal implicit ODE solver guarantees superiority over explicit solvers in numerical stability and computational efficiency. We validate the advantages of proximal implicit solvers over existing popular neural ODE solvers on various challenging benchmark tasks, including learning continuous-depth graph neural networks and continuous normalizing flows.

Learning POD of Complex Dynamics Using Heavy-ball Neural ODEs

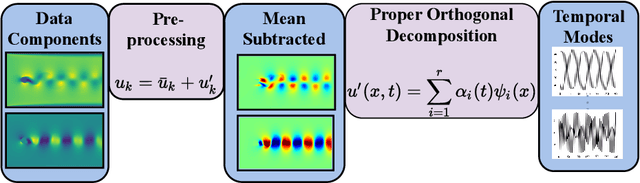
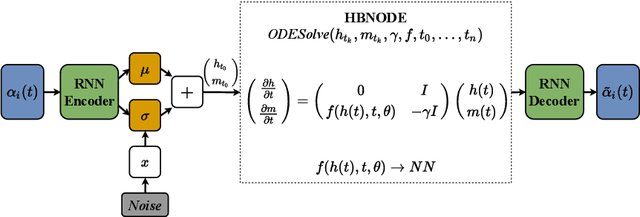
Proper orthogonal decomposition (POD) allows reduced-order modeling of complex dynamical systems at a substantial level, while maintaining a high degree of accuracy in modeling the underlying dynamical systems. Advances in machine learning algorithms enable learning POD-based dynamics from data and making accurate and fast predictions of dynamical systems. In this paper, we leverage the recently proposed heavy-ball neural ODEs (HBNODEs) [Xia et al. NeurIPS, 2021] for learning data-driven reduced-order models (ROMs) in the POD context, in particular, for learning dynamics of time-varying coefficients generated by the POD analysis on training snapshots generated from solving full order models. HBNODE enjoys several practical advantages for learning POD-based ROMs with theoretical guarantees, including 1) HBNODE can learn long-term dependencies effectively from sequential observations and 2) HBNODE is computationally efficient in both training and testing. We compare HBNODE with other popular ROMs on several complex dynamical systems, including the von K\'{a}rm\'{a}n Street flow, the Kurganov-Petrova-Popov equation, and the one-dimensional Euler equations for fluids modeling.